Un jeu d’échec en Ada 2012
Développer un jeu d’échec peut s’avérer être une tâche ardue. Le présent article montre comment la mise en œuvre d’un certain nombre de paradigmes et de services sous-tendus par Ada 2012 permet de rendre cette tâche plus aisée.
Introduction¶
Dans le cadre des formations Ada dispensées par Systerel, un certain nombre d’exercices sont proposés. Tout en étant très techniques, ces exercices ont aussi un côté ludique et c’est par exemple le cas du « jeu d’échec » proposé dans le cadre de notre formation « Ada2012 - Les clés ».
Au travers de cet article nous allons présenter certains éléments permettant de montrer ce qu’amène le langage Ada 2012 dans le développement d’un tel jeu d’échec.
Le code présenté est l’ossature du moteur d’un jeu d’échec basique (1200 ELO) et représentant 2000 lignes de code Ada 2012. La partie graphique est assurée par un client non présenté ici et fourni lors de la formation.
Seules des connaissances basiques des règles du jeu d’échec sont nécessaires pour suivre cet article.
Même si cela ne sera pas présenté dans cet article, l’implémentation utilise aussi des traits spécifiques au langage Ada 2012 tels que :
- Les prédicats statiques,
- Les expressions quantifiées,
- Les pré/post conditions.
Approche objet du problème¶
Un jeu d’échec c’est un ensemble de pièces de types différents (pion, fou, etc.) mais ayant des caractéristiques communes :
- Elles ont une couleur (Blanc ou Noir),
- Elles ont une position sur un échiquier,
- Elles se déplacent sur un même échiquier en respectant des règles précises, certaines étant communes.
On considère donc ici :
- Un échiquier comme un « conteneur » de pièces,
- Une pièce comme un curseur sur ce conteneur.
subtype Case_T is Positive range 1 .. 8 * 8;
-- L'échiquier.
type Plateau_T is array (Case_T) of access Piece_T'Class;
type Echiquier_T is tagged record
Plateau : Plateau_T;
end record;
type Couleur_T is (Noir, Blanc);
-- La classe des pièces
type Piece_T (Couleur : Couleur_T) --> sa couleur
is abstract tagged record
C_ase : Case_T; --> sa position
Echiquier : access Echiquier_T; --> son échiquier
end record;
-- Le poids d'une pièce est utilisé par la fonction d'évaluation (voir suite)
function Poids (Piece : in Piece_T) return Integer is abstract
with Inline => True;
-- on doit connaitre les règles de déplacement d'une pièce
function Deplacement_Valide_Vers (Piece : in Piece_T;
Vers : in Case_T) return Boolean is abstract
with Inline => True;
La fonction à l’échelle de classe Valide_Vers implémente les règles
communes à toutes les pièces quant à leurs déplacements :
function Valide_Vers (Piece : in Piece_T'Class;
Vers : in Case_T) return Boolean is
Plateau : constant Plateau_T := Piece.Echiquier.Plateau;
Resultat : Boolean := True;
begin
if Plateau (Vers) /= null and then
Plateau (Vers).Couleur = Piece.Couleur
then
-- je ne peux pas aller sur une case contenant une pièce de ma couleur
-- je ne peux pas faire du sur place
Resultat := False;
end if;
return Resultat;
end Valide_Vers;
Sachant que chaque pièce devra implémenter sa propre fonction
Deplacement_Valide_Vers (l’abstract ci-dessus) afin de vérifier
la validité de ses déplacements.
Maintenant nous devons définir les pièces de notre échiquier :
type Pion_T is new Piece_T with null record;
overriding
function Deplacement_Valide_Vers (Pion : in Pion_T;
Vers : in Case_T) return Boolean;
overriding
function Poids (Pion : in Pion_T) return Integer is
(if Pion.Couleur = Blanc then -1 else +1) with Inline => True;
Avec ici par exemple :
overriding
function Deplacement_Valide_Vers (Pion : in Pion_T;
Vers : in Case_T) return Boolean is
Resultat : Boolean := Pion.Valide_Vers (Vers);
begin
if Resultat then
Resultat := ... -- test de la validité du mouvement propre au pion
end if;
return Resultat;
end Deplacement_Valide_Vers;
Le cavalier :
type Cavalier_T is new Piece_T with null record;
overriding
function Deplacement_Valide_Vers (Cavalier : in Cavalier_T;
Vers : in Case_T) return Boolean
with Inline => True;
overriding
function Poids (Cavalier : in Cavalier_T) return Integer is
(if Cavalier.Couleur = Blanc then -500 else +500)
with Inline => True;
La dame, le roi, la tour, etc…
Et peupler celui-ci :
Echiquier : aliased Echiquier_T := (Plateau => (1 | 8 => new Tour_T(Noir),
...
57 | 64 => new Tour_T(Blanc),
...
others => null)); --> cases vides
Notre échiquier étant ainsi peuplé, il suffit de déplacer une pièce et la méthode appropriée pour vérifier la validité du déplacement de cette dernière sera appelée par ré-aiguillage.

-- a1(57) a2(49)
if Echiquier.Plateau (57).Deplacement_Valide_Vers (49) then
...
-- a2(49) a3(41)
if Echiquier.Plateau (49).Deplacement_Valide_Vers (41) then
...

-- a3(41) a4(33) CONSTRAINT_ERROR (access check)
if Echiquier.Plateau (41).Deplacement_Valide_Vers (33) then
...
Implémentation de l’IA ¶
L’IA du jeu est mise en œuvre au travers d’un algorithme Mini-Max consistant à calculer successivement tous les coups possibles pour chacun des joueurs. Une fonction d’évaluation permet d’associer une valeur à une situation de jeu pour chaque ½ coup joué. L’ensemble des possibilités va alors créer un arbre des coups possibles :
- La racine de l’arbre représente l’état actuel de la partie (ici Empty_Tree).
- Un nœud représente une situation légale du jeu.
- Les fils d’un nœud sont les situations que l’on peut atteindre à partir de ce nœud en respectant les règles du jeu.
- Une branche représente une séquence de ½ coups légaux dans la partie.
L’analyse de cet arbre (analyse remontante à partir de ses feuilles) permet donc de connaitre le coup initial permettant d’avoir le meilleur score :
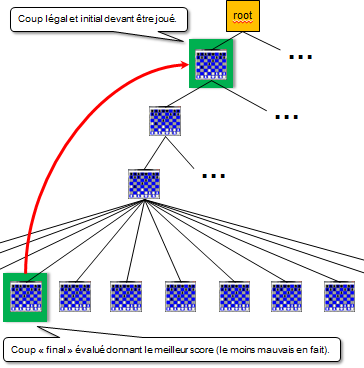
Imaginé en 1928 par Von Neumann, le postulat de base de cet algorithme est que l’adversaire de l’ordinateur jouera toujours le meilleur coup possible.
Cependant, cet algorithme a deux inconvénients :
- Il explore toutes les branches de l’arbre sans aucune forme de distinction entre celles-ci alors que certaines ne produiront de fait aucune opportunité de coups.
- Le nombre d’éléments dans l’arbre explose quand la profondeur augmente. Si on calculait tous les coups possibles avec une profondeur de 100, on obtiendrait un arbre ayant plus d’éléments que de nucléons dans l’univers soit ~$10^{80}$ !
Un algorithme plus efficace tel que Alpha-Bêta (ou élagage Alpha-Bêta) aurait pu être mis en œuvre mais dans le cadre de l’exercice il a été fait le choix de mettre en œuvre le plus simple des algorithmes.
L’arbre des coups a été implémenté en utilisant le nouveau conteneur Ada 2012 Ada.Containers.Multiway_Trees.
Chaque nœud de l’arbre contient les informations suivantes :
- La couleur jouée,
- Le demi-coup joué (De/Vers),
- L’échiquier résultant du demi-coup joué,
- La valeur de cet échiquier (le résultat de la fonction d’évaluation),
type Coup_Possible_T is record
De, Vers : Case_T := Case_T'First;
Couleur : Couleur_T := Blanc;
Valeur : Integer := 0;
Echiquier : Ref_Echiquier_T := null;
end record;
package Pkg_Arbre_Des_Coups is new
Ada.Containers.Multiway_Trees (Element_Type => Coup_Possible_T);
Arbre_Des_Coups : Tree := Pkg_Arbre_Des_Coups.Empty_Tree; --> root
La fonction d’évaluation utilisée ici est proche de :
function Valeur (Echiquier : in Echiquier_T;
Couleur : in Couleur_T) return Integer is
...
begin
for Piece of Echiquier.Plateau loop
if Piece /= null then
Resultat := Resultat + Piece.Poids;
end if;
end loop;
return Resultat + ... ;
end Valeur;
La construction de l’arbre et la remontée de celui-ci se font au travers
des nombreux services proposés par le paquetage Ada.Containers.Multiway_Trees.
Conclusion¶
Le langage Ada 2012 a apporté de nouvelles fonctionnalités telles que :
- La programmation par contrat et la notion d’aspects,
- De nouvelles formes d’expressions et de prédicats,
- La prise en charge des architectures SMP,
- Les itérateurs,
- Une extension de l’environnement prédéfini,
- Des améliorations diverses et variées.
Hormis des corrections sémantiques ou des améliorations « esthétiques », Ada 2012 met comme ses « prédécesseurs » particulièrement l’accent sur de nouveaux traits permettant de garantir au mieux la sécurité et l’intégrité des applications développées tout en embrassant les nouvelles technologies telles que la technologie SMP.
Même si l’implémentation présentée ici aurait pu être développée dans un autre langage, le fait de l’avoir réalisée en Ada 2012 a contribué grandement à ce que celle-ci soit concise, lisible et fiable.

Commentaires